事务并发调度、冲突可串行化以及依赖图
梳理事务并发调度、冲突可串行化以及依赖图的定义,整理这些定义的关系脉络,并最终解答一个问题:“事务并发调度结果正确与否,为什么可以通过检测依赖图无环来验证?”。
上述问题,可以拆分成三个子问题:
- 为什么事务并发调度是要等价于串行化调度?
- 为什么一个并发调度序列得是冲突可串行化,跟串行化有什么关系?
- 为什么一个并发调度序列所构建的依赖图得是无环的,跟冲突可串行化有什么关系?
关键词:并发调度、串行化调度、冲突可串行化、依赖图
事务并发调度(Concurrent Schedules)
数据库事务并发调度,指的是,数据库系统能够交替调度不同事务的不同操作。
示例如下:
- T1 负责转账,从账户 A 转账100元给 账户 B
- T2 是年度计息,要给每个账户加利息6%
左侧就是并发调度序列,右侧就是串行化调度。
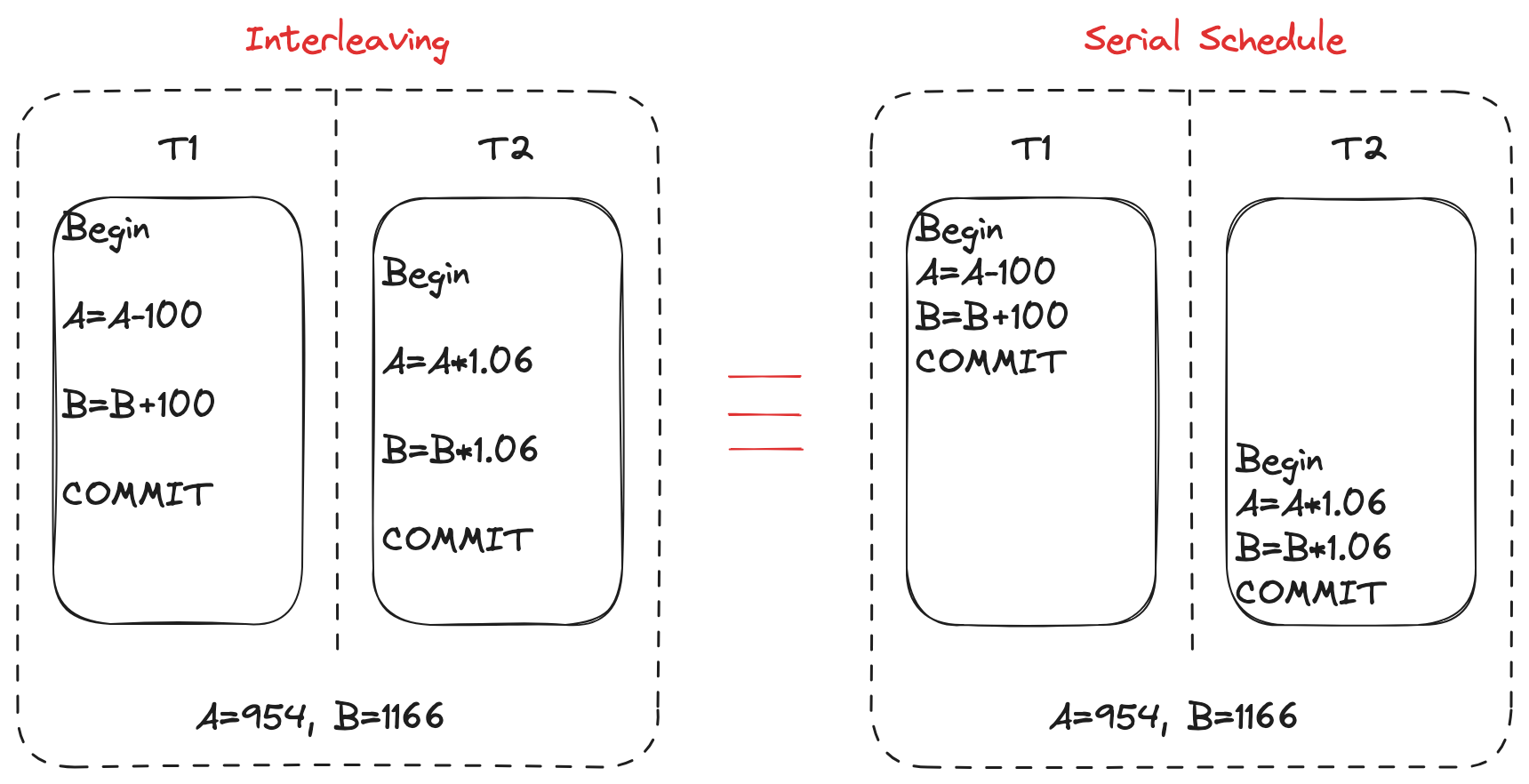
可以看出左侧并发调度的结果,等价于右侧串行化调度 \(T1 \rightarrow T2\) 的结果。
再看另外一个并发调度序列:
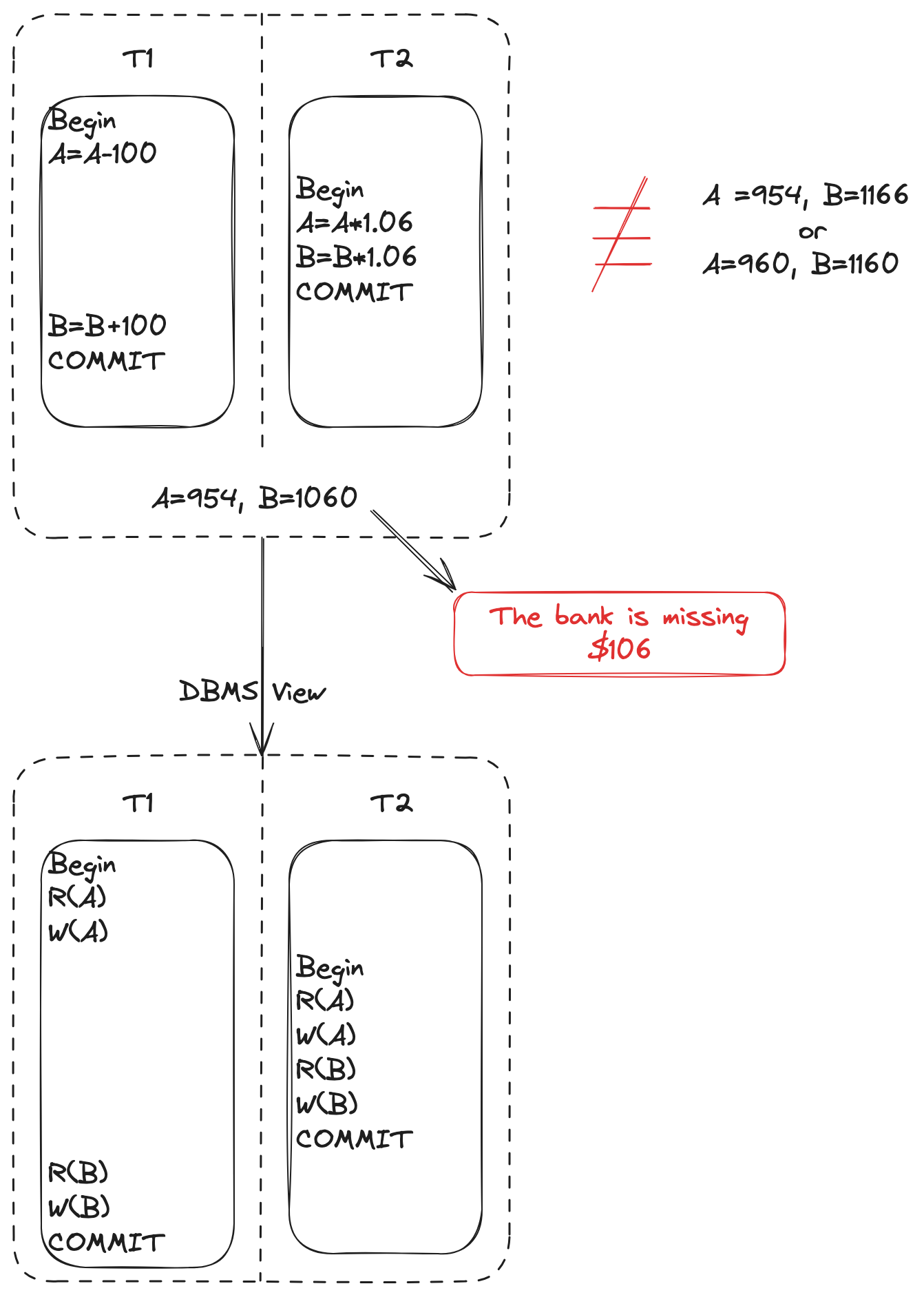
可以发现这次的调度序列的执行结果并不等于任何一种串行化调度序列的结果:{\(T1 \rightarrow T2\), \(T2 \rightarrow T1\)}。
而且,T2 读取了 T1 修改了一半的数据,并在此基础上做了自己的修改,该调度序列违背隔离性要求,最终造成“脏写(Dirty Write)”问题 : T2 覆盖了 T1 未提交的写入结果。
既然两种并发调度序列会得到不同的结果。那么,如何判定一个调度序列最终结果是正确的?如何判断上述例子中,第一个并发调度是正确的,而第二个就是错误的呢?
再回答这个问题之前,需要先了解另外一种调度方式,也就是串行化调度。
事务串行化调度(Serial Schedule)以及关于“正确”的定义
数据库系统,完全不交替调度不同事务的不同操作,按照顺序执行每一个事务,就称为“串行化调度(Serial Schedule)”,需要注意的是这里并不要要求多个事务严格按照某一顺序。
比如,数据库系统收到并发事务: T1、T2、T3,那么三个事务的串行化调度序列,可以有以下六种组合:{\(T1 \rightarrow T2 \rightarrow T3\), \(T1 \rightarrow T3 \rightarrow T2\), \(T2 \rightarrow T1 \rightarrow T3\), \(T2 \rightarrow T3 \rightarrow T1\), \(T3 \rightarrow T2 \rightarrow T1\), \(T3 \rightarrow T1 \rightarrow T2\)}。
重点来了,按照这六种组合中的任意一种,执行得到的结果,对于数据库系统来说都是合法的。只要这三个事务本身没有破坏一致性的操作,那么任何一种组合,都不会破坏数据库系统的一致性,并且执行期间不会出现任何违背隔离性错误的情况。那对于数据库系统来说,自然都是正确的。
比如,以下两种调度都是合法的、正确的:
- 第一种是,\(T1 \rightarrow T2\) ,先执行转账,再计息
- 第二种是,\(T1 \rightarrow T2\),先执行计息,再转账
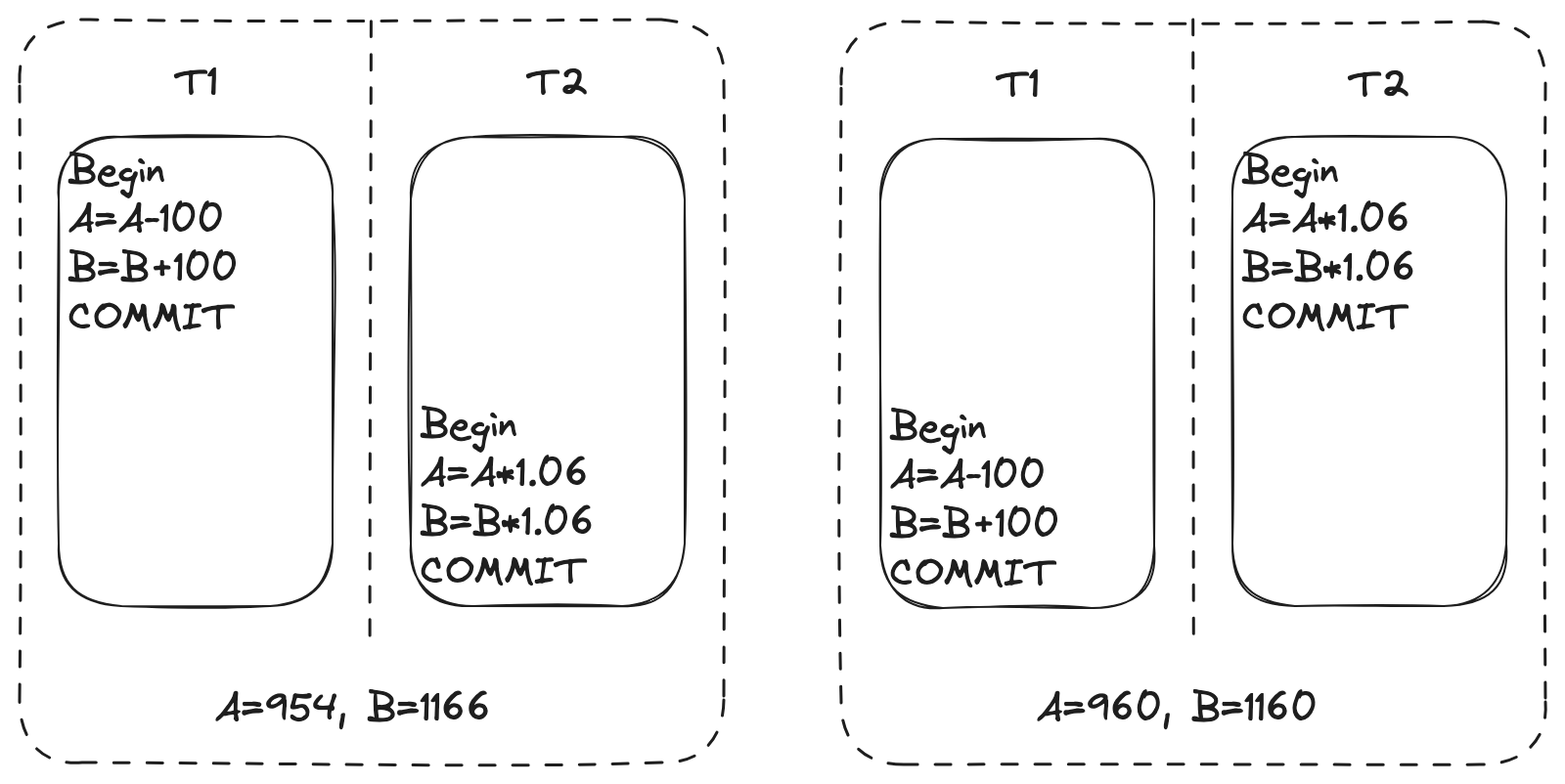
虽然,两种调度序列,最终得到的 A 和 B 结果不一样,但每次执行都是基于当时已提交的结果做的判断,同时执行过程中并没有依赖其他事务的中间结果,所以整个过程没有出现违背隔离性错误。这两个调度序列都是合法,它们的结果也都是正确的。
事务等价调度(Equivalent Schedules)和可串行化调度(Serializable Schedule)
事务等价调度,对于数据库系统中的数据状态,执行第一种调度的结果,跟执行第二种调度的结果一样。那么不管各自调度中间是经过什么样的运算,都可以认为这两种调度是等价的。
比如以下三个调度序列,都让数据库状态从 x 变成 y,那就认为这三个调度序列是等价的:
基于上述对于结果正确的定义,答案就很简单了,所谓“正确的”并发调度序列,就是能跟串行化调度等价的调度序列。
至此,已经回答了第一个子问题,一个并发调度序列,能够等价于一个或某几个串行化调度序列,那么我们就称该调度为可串行化调度(Serializable Schedule),它的执行结果一定是正确的,不会出现违背隔离性错误的情况。
接下来在回答第二个子问题之前,需要先梳理清楚另外一个概念,那就是冲突可串行化(Conflict Serializable)。
冲突可串行化(Conflict Serializable)
一个调度序列,如果说是冲突可串行化(conflict serializable),那么该调度序列冲突等价(conflict equivalent)某一个串行化调度(serial schedule)。
更加直观的描述是,如果一个调度序列是冲突可串行化(conflict serializable),那么可以通过交换序列中非冲突操作,得到一个串行化调度序列。
这里出现了两个新的概念:冲突操作、冲突等价。
冲突操作
在事务并发地交替调度的过程中,可能出现以下三种读写冲突:
- 读-写冲突(R-W)
- 写-读冲突(W-R)
- 写-写冲突(W-W)
当然,这里还隐含了一个条件,那就是不同事务操作了同一个数据对象。为此可以总结冲突操作三个条件:
- 操作归属于不同事务
- 操作同一个数据对象
- 至少有一个操作是写操作
这些读写冲突没有得到解决,就会导致出现各种违背隔离性错误,关于违背隔离性错误的细节查看另外一篇文章:浅谈数据库事务违背隔离性错误,这里不再展开讨论。
冲突等价
两个调度序列可判定为,冲突等价(conflict equivalent),当且仅当:
- 涉及相同事务、相同操作,并且
- 每对冲突操作都以相同的方式排序
假设有两个并发事务,它们的操作如下:
\[ T1: R_1(A),W_1(A),R_1(B),W_1(B) \]
\[ T2: R_2(A),W_2(A),R_2(B),W_2(B) \]
现在有两个调度序列:
\[ S1: R_1(A),W_1(A),R_2(A),W_2(A),R_1(B),W_1(B),R_2(B),W_2(B) \]
\[ S2: R_1(A),W_1(A),R_1(B),W_1(B),R_2(A),W_2(A),R_2(B),W_2(B) \]
观察 \(S1\) 可以发现,一共存在如下冲突操作以及它们出现的顺序:
- W1(A) - R2(A)
- R1(A) - W2(A)
- W1(A) - W2(A)
- W1(B) - R2(B)
- R1(B) - W2(B)
- W1(B) - W2(B)
再看 \(S2\) ,会发现有着跟 \(S1\) 相同的冲突操作并且这些冲突操作的出现顺序是一样的。
鉴于,\(S1\) 和 \(S2\),有着以下三个特性:
- 相同事务,都是 T1 、T2
- 相同操作,都是对 A 和 B 两个数据对象,执行一次读和一次写
- 有着相同的冲突操作,并且这些冲突操作的顺序是一样的。
至此,可以说,\(S1\) 和 \(S2\) 是冲突等价的。
再观察 \(S2\) 可以发现,它就是串行化的调度 T1 和 T2 两个事务,所以其本身是串行化调度序列。那也就是说, \(S1\) 实际上是冲突等价于一个串行化调度序列,,因此可以说 \(S1\) 是冲突可串行化。
冲突可串行化是可串行化的充分非必要条件
从冲突可串行化和可串行化的定义来看:一个调度序列,如果可以冲突可串行化,那就一定等价于某一个串行化调度序列,那必然是可串行化的。
但是,反过来。如果一个调度序列是可串行化的,但它不一定是冲突可串行化的。
观察以下调度序列:
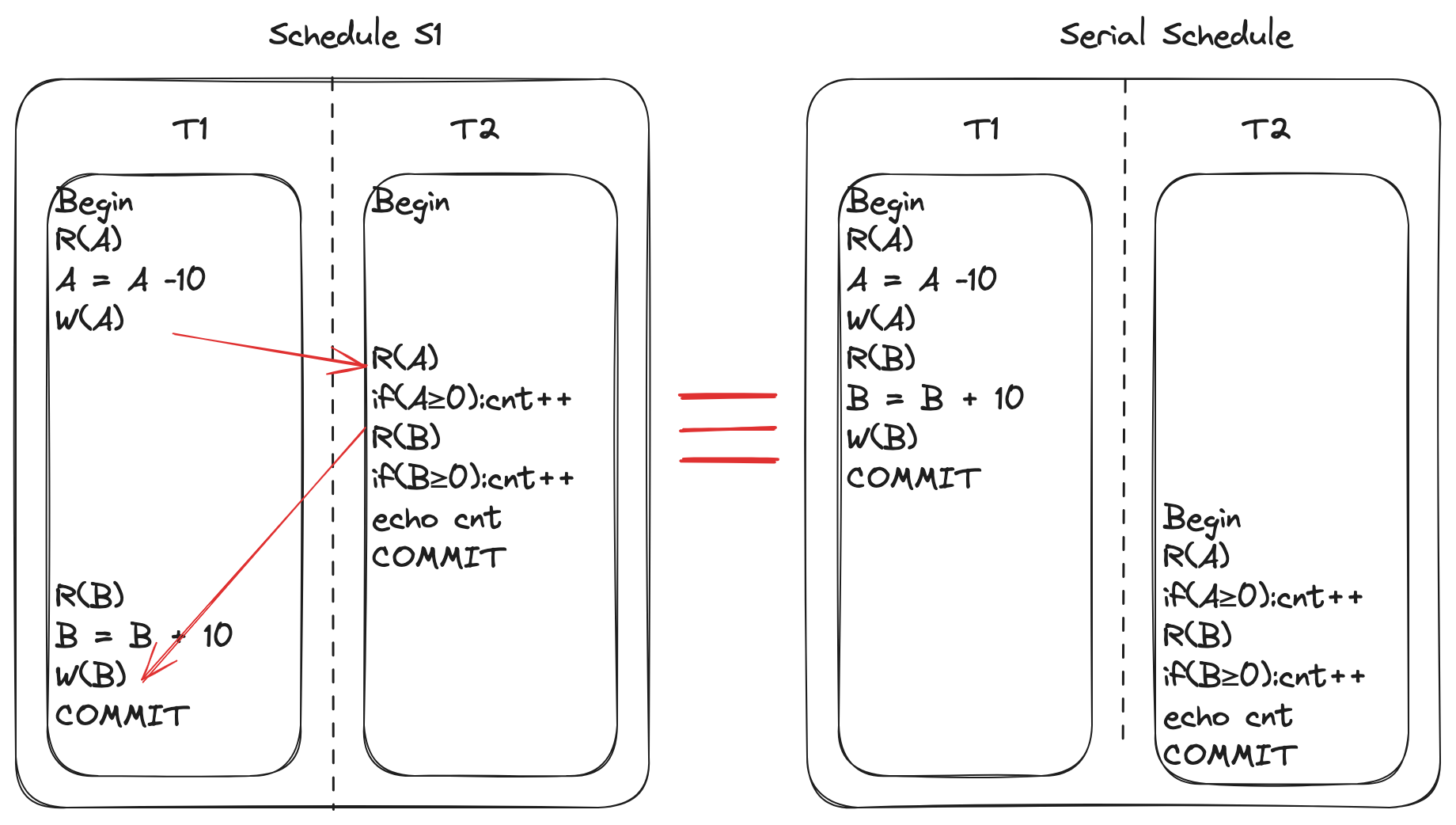
左侧的并发调度序列如下所示:
\[ S1: R_1(A)W_1(A)R_2(A)R_2(B)R_1(B)W_1(B) \]
存在以下冲突操作:
- W1(A) - R2(A)
- R2(B) - W1(B)
没办法通过交换非冲突操作来得到一个串行化的调度序列,也就是该调度序列在现今的数据库系统实现中,只能是阻塞事务 T2 直到事务 T1 提交。
但是,我们可以发现,如果直接并发地执行事务 T2,根本不会影响事务 T2 的结果,也不会影响事务 T1 的结果。也就是说,该调度序列,直接并发执行实际上是可以等价于右侧的串行化调度序列的结果,即 \(T_1 \rightarrow T_2\)。只是,目前的程序模型不支持这么做。
总之,一个并发调度序列,如果是冲突可串行化,那么它必然是可串行化,反之不然。冲突可串行化是可串行化的充分非必要条件。
至此,我们就回答了第二个子问题:判断并发调度序列是否正确,可以通过检验其是否冲突可串行化。如果可以,那就说明该调度序列是可串行化,它的执行结果是正确。
一种低效的实现方案:交换非冲突操作
现在,问题已经转换为,“如果要验证一个事务并发调度序列的结果是正确的,那么只需要验证该调度序列是冲突可串行化的”。
那么如何验证一个调度序列是否冲突可串行化呢?
有一种低效实现方案:通过交换序列中非冲突操作,然后看看最后能否得到一个串行化调度序列。
还是上述的例子,考虑以下调度序列:
\[ S1: R_1(A),W_1(A),R_2(A),\textcolor{red}{W_2(A),R_1(B)},W_1(B),R_2(B),W_2(B) \]
观察 \(S1\) 序列中, \(W_2(A)\) - \(R_1(B)\) 是相邻的非冲突操作,可以交换这两个操作的执行顺序,得到以下新的调度序列:
\[ S1’: R_1(A),W_1(A),R_2(A),\textcolor{red}{R_1(B),W_2(A)},W_1(B),R_2(B),W_2(B) \]
此时,\(S1\) 和 \(S1’\) 是冲突等价的,那么继续交换序列中存在的非冲突操作对:
- \(R_2(A)-R_1(B)\)
- \(W_2(A)-W_1(B)\)
- \(R_2(A)-W_1(B)\)
得到以下最终的调度序列:
\[ S1^{final}: R_1(A),W_1(A),R_1(B),W_1(B),R_2(A),W_2(A),R_2(B),W_2(B) \]
观察 \(S1^{final}\) 可以发现,该调度序列实际上就是两个事务串行化执行。
至此,我们就可以说 \(S1\) 是冲突可串行化的,该并发调度序列的结果会是正确的。
当然,这种做法很蠢,因为每提交一个操作,就要重复上述过程。效率慢,所以,需要更加高效的实现方案。
为此,我们引出了依赖图的设计。
依赖图(Dependency Graph)
构造算法如下:
- 一个事务就是一个节点(Node)
- 如果满足以下条件,则绘制一条从 \(T_i\) 指向 \(T_j\) 的边(Edge):
- 来自事务 \(T_i\) 的操作 \(o_i\) 和来自事务 \(T_j\) 的操作 \(o_j\) 冲突
- 并且操作 \(o_i\) 发生在操作 \(o_j\) 之前
一个调度序列,是冲突可序列化的,当且仅当其依赖图是无环的。换言之,冲突可串行化是依赖图无环的充分必要条件。
关于这一点的数学证明,这里不展开,感兴趣的可以自行查看: Proof of correctness of the precedence graph test。 一共分为两个步骤来证明:
- 反证法
- 归纳推理
示例如下,一共有三个事务,T1、T2、T3:
- T1 的 R(A) 操作跟 T3 的 W(A) 操作冲突,并且 T1 发生在 T3 之前,所以 T1 指向 T3
- T2 的 W(B) 操作跟 T1 的 R(B) 操作冲突,并且 T2 发生在 T1 之前,所以 T2 指向 T1
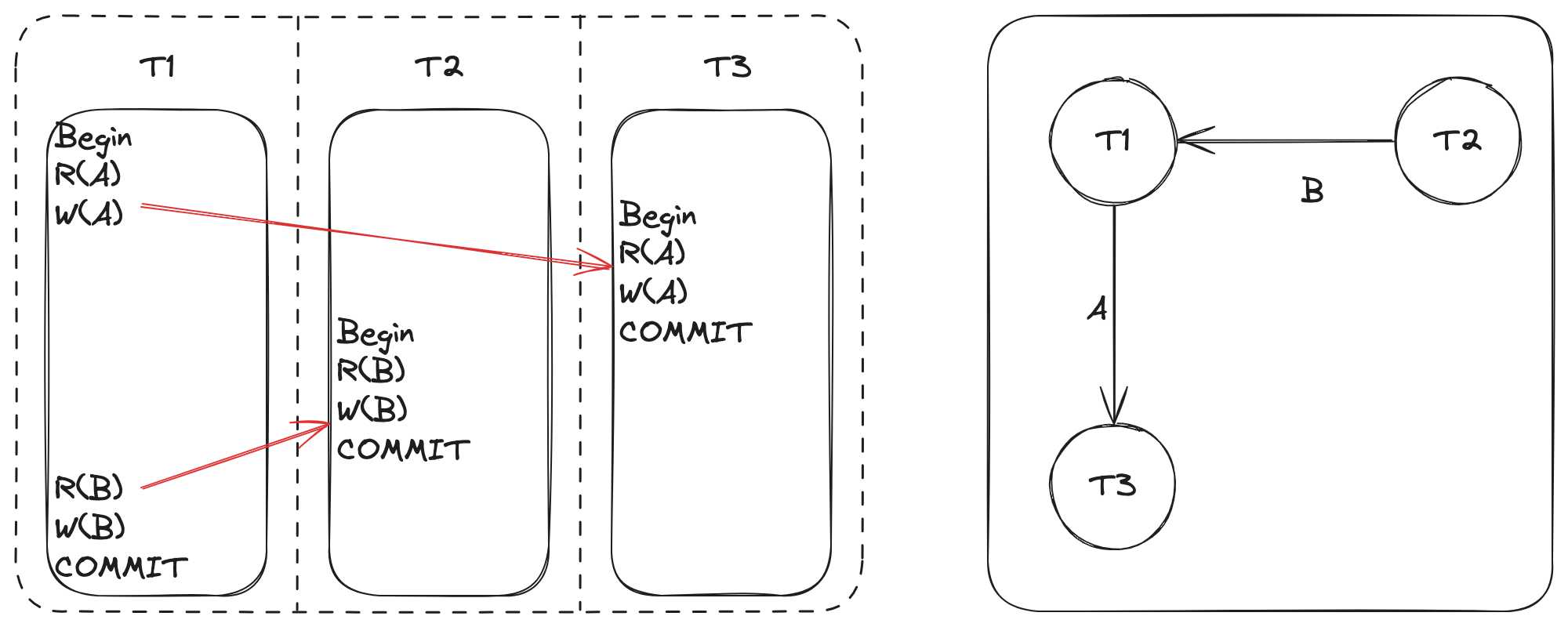
那么,以上调度序列是否等价于某个串行化调度序列呢?是的,可以等价于 \(T2 \rightarrow T1 \rightarrow T3\) 串行化序列。
直观上理解,一张图上的节点和边,构建了冲突操作的顺序。如果在依赖图中存在环,那么就没办法将所有冲突操作串行(想象连成一条直线),因为没办法交换它们的顺序。
针对上述例子,再增加一个数据对象 C:
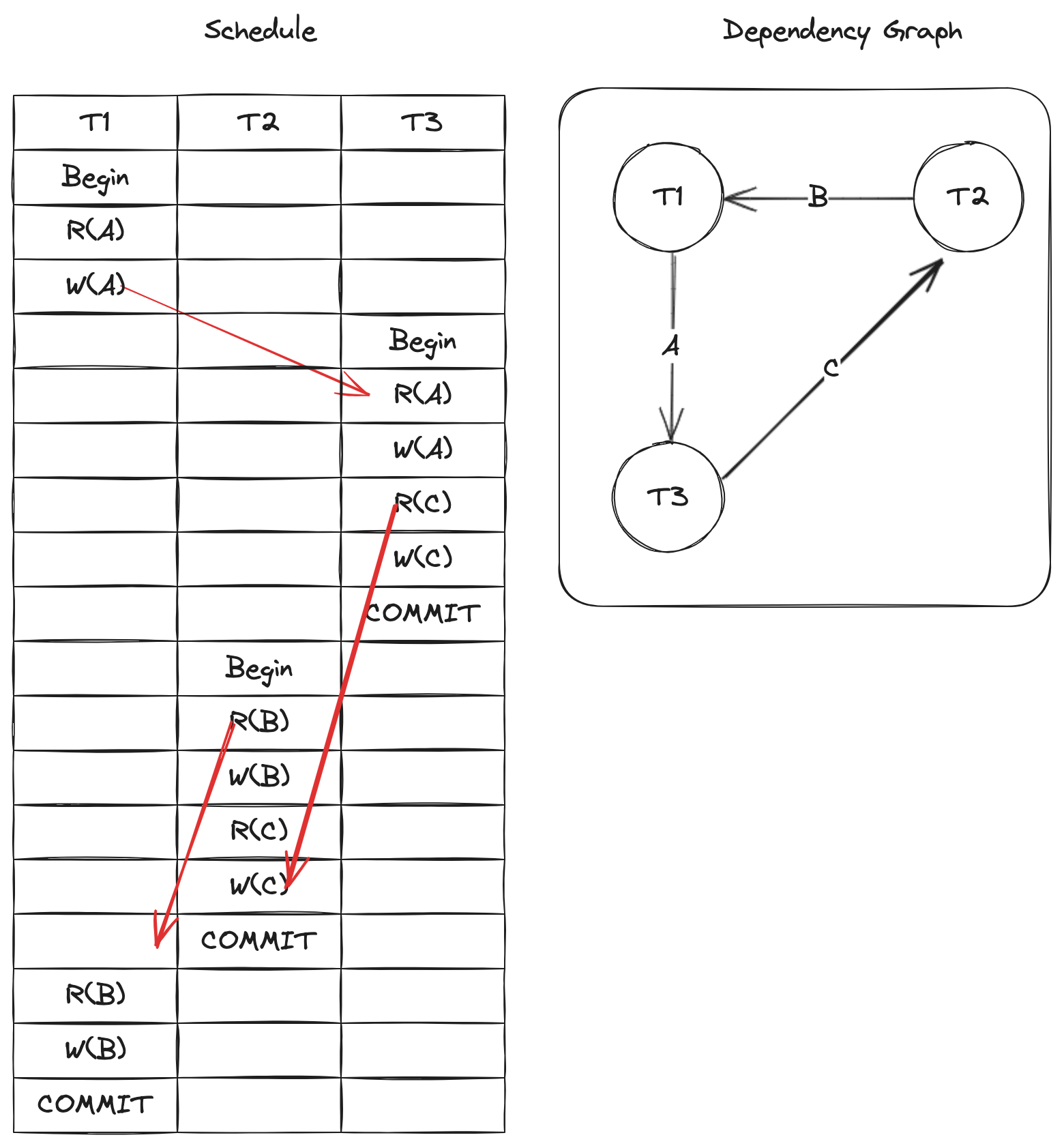
如果从调度序列来看,就是:
\[ S1: R_1(A)W_1(A)R_3(A)W_3(A)R_3(C)W_3(C)R_2(B)W_2(B)R_2(C)W_2(C)R_1(B)W_1(B) \]
从图中可以看出:
- 由于 T3 和 T2 之间,在数据对象 C 上冲突操作,没办法将 T2 的 \(R_2(C)W_2(C)\) 交换到 T3 之前
- 由于 T2 和 T1 之间,在数据对象 B 上冲突操作,没办法将 T1 的 \(R_1(B)W_1(B)\) 交换到 T2 之前
- 由于 T1 和 T3 之间,在数据对象 A 上冲突操作,没办法将 T3 的 \(R_3(A)W_3(A)\) 交换到 T1 之前
最终,整个序列没办法通过交换非冲突操作,转换为一个串行化的调度序列。该调度序列不是冲突可串行化的。
总结
针对一开始提到的三个问题,我们给出以下的回答:
- 一个并发调度序列,如果它的结果等价于串行化调度结果,它的结果就是正确的。
- 一个并发调度调度序列,如果是冲突可串行化,那么它必然是可串行化。
- 一个并发调度调度序列,是冲突可串行化,当且仅当它的依赖图是无环的。
为此,我们可以得到以下结论:
在事务并发调度的实现中,只要我们能够证明该调度序列所构建的依赖图是无环的,那么我们就可以证明该调度序列是正确的,执行期间不会违背隔离性。
依靠数学转化思维,我们将事务并发调度正确性问题,层层递进,最终转换为判断一个图是否有环的问题。证明后者,就能验证前者的正确性。